去年或前年讀到的文章,今日強迫自己整理記下。
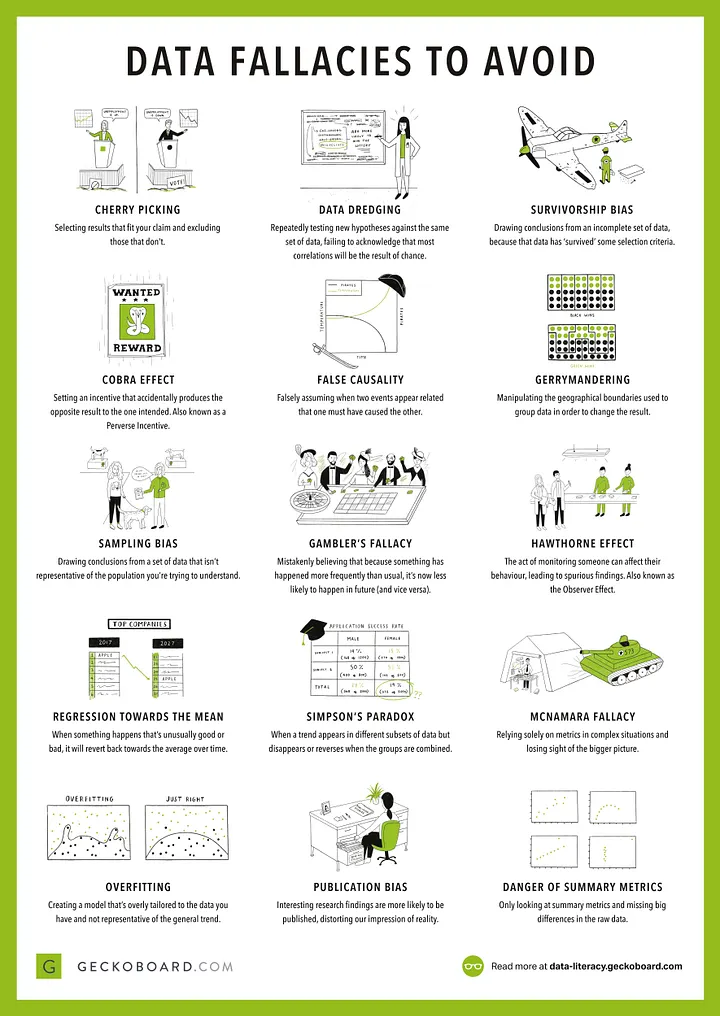
【資料科學的15個常見謬誤】 / 李耕銘
-
Cherry picking 單方論證
只說自己想要說的。
舉例來說就是採櫻桃的工人只採好的櫻桃,會讓你覺得所有的櫻桃都是好的。
或只說單一支持/反對的論點,忽略其他不提,這讓我想到公視對「帶風向」這詞的定義也是如此。 -
Data dredging 資料捕撈/資料挖泥
一般研究都是先提出假說,再透過實驗設計、執行與最後的數據來證實或推翻假說,而 Data dredging 指的是順序顛倒,有了資料後再去看這資料有甚麼表現比較好的特性去選擇研究主題。例如一開始想研究翹課頻率跟成績的關聯,但後來發現沒關係,可是跟抽菸有關,於是就把題目直接改成翹課與抽菸的關聯。
不得不說這種情況在研究所應該還蠻常見的XD
-
Survivor bias 倖存者偏差
這個大家都應該聽過二戰戰鬥機的例子,軍方在討論如何改善戰機的存活率時,若只觀察成功返回的飛機彈孔位置就認為這些地方比較常中彈是不對的,因為這些彈孔代表的其實是中彈還是可以飛行的位置。至於中彈後會導致直接損毀的位置是觀察不到的(因為都墜毀了)。
-
Cobra effect 眼鏡蛇效應
針對問題的解決方案,反而是讓該問題更惡化。這個詞的來源是英國政府為了減少當初殖民印度時的眼鏡蛇數目,就公布一項規定:殺蛇可換到不少錢,於是就開始興起養眼鏡蛇換賞金的風潮,隨後英國政府也意識到這件事情便把賞金取消。
取消之後呢?那些養眼鏡蛇的馬上都把所有的眼鏡蛇給放生了,於是野外的眼鏡蛇又更多了XDD
-
False causality 因果謬誤
觀察到 A 事件發生在 B 事件之後,或是 A、B事件有相關性,就認為A、B事件互為因果, 之前聽過的例子是友人調查巧克力食用量與健康的關係,發現世界上巧克力食用量越高的地區,健康情形也越好。但這代表巧克力對健康有益嗎?
不,因為巧克力食用越多,通常代表該區域的經濟狀況也較好。 -
Gerrymandering 傑利蠑螈
來自於美國曾經發生的事件,透過選區劃分可以增加/減少特定政黨的形式,導致為了操控席次而進行各種怪異的選區畫分法,結果就是有一個選區的形狀特別奇怪像蠑螈而得名。在資料科學裡就是改變資料的分組方式藉此操縱最後的結果。
-
Sampling bias 取樣誤差
一開始在抽樣的人群便無法代表母體,比如說你在台北市大安區街頭抽樣每個人的薪水,就拿這些人的薪水代表全台灣的人,從無法代表母體分布的樣本中抽樣會導致的誤差。 -
Hawthorne effect 霍桑效應
在霍桑工廠進行的實驗,當初的實驗想要知道那些變因會影響員工的生產力,但意外發現觀察者知道自己被觀察時就會改變行為傾向。當長官給予下屬關懷或照顧時,員工的生產力提升也可以用霍桑效應解釋。 -
Gambler’s fallacy 賭徒謬誤
想像一個在賭場賭骰子的狀況,如果連續出現了很多次 6,就認為下一次一定會/不會再是 6,或是認為某個點數很久沒出現所以下次一定會出現的想法。因為就機率來看公正骰子出現的點數機率都是 1/6。 -
Regression toward the mean 回歸均值
單一一次的表現都會不可避免地受到隨機誤差影響,可能增加也可能降低,但如果次數一大,原本的差異就會回歸到平均而被弭平,比方說我發現某個方法在第一輪時預測狀況特別好,但多做幾個 Epoch 後,這個方法的優勢就會被弭平。另一個例子就是股價短期會收到隨機波動的影像,所以兩個公司表現差不多的時候,股價短期內卻有可能呈現一個上漲、一個下跌,但只要觀察時間長,這兩隻公司的股價最終還是會回到均值。
-
Simpson’s paradox 辛普森悖論
如果我們有兩種資料:A、B,兩種評分方式:甲、乙,不管在甲乙這兩種評分方式下都是 A 勝出,但不代表最終結果 A 一定會勝出。每個評估下都強的資料,在綜合評估的時候不一定會強。 -
Mcnamara fallacy 麥納馬拉謬誤
過度使用簡化的數據來描述事件的發生傾向,源自於越戰有人試圖把戰爭的勝利與否加以數據化,其中最重要的兩個變量便是擊斃敵軍的數目和我方人員的損失,但這樣做並沒有考慮到政治情勢、游擊戰、民意的波動。另一個例子就是醫療,如果我們只用存活率/存活時間來評估療效,那麼存活的品質就會被忽略,變成痛苦地活了很久。
-
Overfitting 過擬和
該模型能夠在 train data 中有很好的預測性,但在 test data 裡的表現很糟糕,多半是因為訓練過頭導致,我想大家都了解所以就不在贅述。 -
Publication bias 發表偏差
只有有趣或顯著的結果/現象會被當作文獻發表在學界,所以常常看學術論文的人可能會誤會這些現象常常發生,進而對這世界產生誤解。 -
Danger of summary metrics
如果我們用統計數據來描述資料,就會失去資料的分布特性,比方說這兩筆資料的平均數是一樣的:1 3 5 v.s. 3 3 3但是分布卻完全不一樣!所以要小心用統計數據表示數據時可能會造成的資料遺失!